Ⅰ. 정수와 유리수
1. 부호를 가진 수
기호 를 덧셈, 뺄셈 기호와 구별해서 부호라고 한다.
여기서, ' '를 양의 부호, ' '를 음의 부호라고 한다.
양수 : 0보다 큰 수 : +8, +3, +0.5, ....
음수 : 0보다 작은 수 : -3, -1, -1.5, ....
▶ +3에서의 양의 부호 "+" 와 -4에서의 음의 부호 "-" 는 그 모양이 덧셈, 뺄셈의 기호와 같지만 그 의미는 다르다.
2. 정수와 유리수
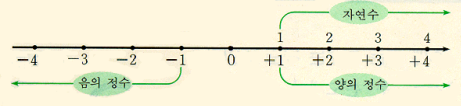
유리수 : 분모와 분자가 모두 정수인 분수로 나타낼 수 있는 수(단, 분모는 0이 아님)

▶ +2:"양의 정수 이" 또는 "양수 이" 또는 "플러스 이" 라고 읽는다
▶ -4:"음의 정수 사" 또는 "음수 사" 또는 "마이너스 사" 라고 읽는다
▶모든 유리수는 수직선 위의 점으로 나타낼 수 있다.
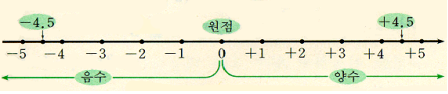
3. 절대값
수직선 위에서 어떤 수를 나타내는 점과 원점 사이의 거리로 양수, 음수에서 부호 +/-를 없앤 수
▶절대값이 $a$인(단, $a>0$) 수는 $+a$와 $-a$의 두 개가 있다.
▶l0l=0
4. 수의 대소 관계
․ 양수는 0보다 크고, 음수는 0보다 작다. 즉, 양수는 음수보다 크다.
․ 두 양수에서는 절대값이 큰 수가 크다.
․ 두 음수에서는 절대값이 큰 수가 작다.
$a+b=b+a$ (교환법칙)
$(a+b)+c = a+(b+c)$ (결합법칙)
▶ 대소관계는 부등호 "<,>" 또는 "≤,≥"를 사용하여 나타낸다.
$x$는 $a$보다 크다 : $x>a$
$x$는 $a$보다 작다 : $x<a$
$x$는 $a$보다 크거나 같다 : $x\geq a$
$x$는 $a$보다 작거나 같다 : $x\leq a$
Ⅱ. 유리수의 연산
1. 유리수의 덧셈
▶ 부호가 같은 두 수의 덧셈 : 두 수의 절대값의 합에 공통인 부호를 붙인다.
▶ 부호가 다른 두 수의 덧셈 : 두 수의 절대값의 차에 절대값이 큰 수의 부호를 붙인다.
▶ 덧셈의 계산법칙
▶ 절대값이 같고 부호가 다른 수의 합은 0이다.
2. 유리수의 뺄셈
▶유리수의 뺄셈은 빼는 수의 부호를 바꾸어 더한다.
▶덧셈과 뺄셈이 혼합된 경우에는 뺄셈을 덧셈으로 고친 후 양수는 양수끼리,
음수는 음수 끼리 모아서 계산한다.
▶부호가 없는 수는 "+"가 생략된 것이다.
3. 유리수의 곱셈과 나눗셈
▶ 부호가 같은 두 수의 곱셈 : 각 절대값의 곱에 양의 부호 를 붙인다.
▶ 부호가 다른 두 수의 곱셈 : 각 절대값의 곱에 음의 부호 를 붙인다.
▶임의의 수와 0 과의 곱은 항상 0 이다.
▶곱셈의 계산법칙
$a\times b=b\times a$ (교환법칙)
$(a\times b)\times c=a\times (b\times c)$ (결합법칙)
$a\times (b+c)=a\times b+a\times c$ (분배법칙)
4. 유리수의 나눗셈
▶ 부호가 같은 두 수의 나눗셈 : 두 수의 절대값의 나눗셈의 몫에 양의 부호(+)를 붙인다.
▶ 부호가 다른 두 수의 나눗셈 : 두 수의 절대값의 나눗셈의 몫에 음의 부호(-)를 붙인다.
▶유리수의 나눗셈은 나누는 수의 역수를 곱한 곱셈과 같다.
▶곱셈과 나눗셈의 혼합된 식은 곱셈만의 식으로 고쳐서 계산한다.
▶부호 결정 : 셋 이상의 수의 곱셈에서 부호는, 짝수 개의 음수의 곱이면 양수,
홀수개의 음수의 곱이면 음수로 정한다.
▶역 수 : 두 수의 곱이 1이 될 때, 한 수를 다른 수의 역수라고 한다.
5. 복잡한 식의 계산
▶ 거듭제곱이 있으면 이것을 가장 먼저 계산한다.
▶ 소괄호 → 중괄호 → 대괄호 순으로 한다.
▶ 곱셈, 나눗셈을 먼저 계산하고 덧셈, 뺄셈은 나중에 한다.
'생활공학 > 중등수학' 카테고리의 다른 글
| 다항식 관련 용어 (0) | 2021.05.09 |
|---|---|
| 중1) 1-3 문자와 식의 계산 (3) | 2020.11.27 |
| 중1) 1-1 자연수의 성질 (0) | 2020.11.18 |


댓글