1절 부정적분
함수 $f(x)=x^2$의 도함수는 $f'(x)=2x$이다. 거꾸로 함수 $F$의 도함수가 $2x$ 라면 $F$는 어떤 함수인지 알 수 있을까? $x^2$을 미분하면 $2x$가 되는 것을 알고 있으므로
$$F(x)=x^2$$
이라고 할 수 있다. 그러나 미분의 경우와는 달리 이런 성질을 갖는 함수는 무수히 많이 있다. 임의의 상수 $C$에 대하여
$$(x^2+C)'=2x$$
이므로 다음과 같은 형태의 함수
$$F(x)=x^2+c$$
는 모두 도함수가 $2x$이다.
역도함수
일반적으로 주어진 함수 $f$에 대하여
$$F'(x)=f(x)$$
가 되는 미분가능한 함수 $F(x)$를 $f(x)$의 역도함수(antiderivative)라고 한다. 예를 들어 $2x$는 $x^2$의 도함수이고 $x^2$은 $2x$의 역도함수이다. $F(x)$가 $f(x)$의 역도함수라면 $F(x)+C$도 $f(x)$의 역도함수가 된다. 또한 $G(x)$가 $f(x)$의 다른 역도함수라면
$$(G(x)-F(x))'=f(x)-f(x)=0$$
이므로 $G(x)-F(x)$는 상수함수가 된다. 따라서 모든 $f$의 역도함수는
$$F(x)+C$$
의 꼴로 쓸 수 있다. 함수 $f(x)$의 역도함수의 집합을 부정적분(indefinite integral)이라고 하고
$$\int f(x)dx$$
로 나타낸다. 그러나 집합 기호는 사용하지 않으며 다음과 같이 이해하기로 한다.
$$F'(x)=f(x)\quad\Leftrightarrow\quad\int f(x)dx=F(x)+C\qquad (6.1)$$
여기서 함수 $f(x)$를 피적분함수(integrand), $C$를 적분상수(constant of integration)라고 한다. 적분상수 $C$에 대하여 연산을 한 결과는 다시 $C$로 쓰기로 한다. 예를 들어
$$2\int f(x)dx=2F(x)+2C=2F(x)+C$$
로 쓴다. 일반적인 연산에서라면 위의 식에서 $C=0$이 된다. 그러나 적분상수는 일반적인 실수를 나타내는 수임을 상기하고 새로운 적분상수($C'$이나 $C_1$ 등)을 사용하는 대신 계속 적분상수 $C$로 나타내기로 한다.
식(6.1)은 다음과 같이 바꾸어 쓸 수 있다.

여러 함수의 부정적분
$n\neq-1$일 때 $(x^{n+1})'=(n+1)x^n$이므로
$$(\frac{1}{n+1}x^{n+1})'=x^n$$
이다. 따라서 다음 부정적분을 얻는다.
$$\int x^ndx=\frac{1}{n+1}x^{n+1}+C$$
$x^{-1}$의 부정적분은
$$(log\;|x|)'=\frac{1}{x}$$
에서
$$\int\frac{1}{x}dx=log\;|x|+C$$
임을 알 수 있다.
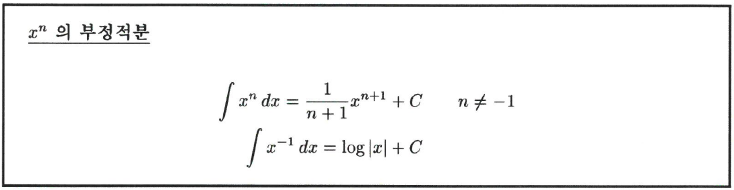
지수함수의 미분법칙으로부터
$$(e^x)'=e^x\quad\Leftrightarrow\quad\int e^xdx=e^x+C$$
이다. 또한
$$(a^x)'=a^xlog\;a$$
이므로
$$(\frac{a^x}{log\;a})'=a^x$$
이다. 따라서
$$\int a^xdx=\frac{a^x}{log\;a}+C$$
이다.

삼각함수의 미분법으로부터는 다음 부정적분을 얻는다.

부정적분의 성질
$F(x),G(x)$가 각각 연속함수 $f(x),g(x)$의 역도함수라고 하자. 그러면
$$F'(x)=f(x),\quad G'(x)=g(x)$$
이므로 임의의 상수 k에 대하여
$$\begin{align*} [kf(x)]'=& kF'(x) = kf(x) \\
[F(x) \pm G(x)]'=&F'(x)\pm G'(x)
\\=&f(x)\pm g(x)
\end{align*}$$
이다. 따라서 부정적분에 대한 다음 공식이 성립한다.
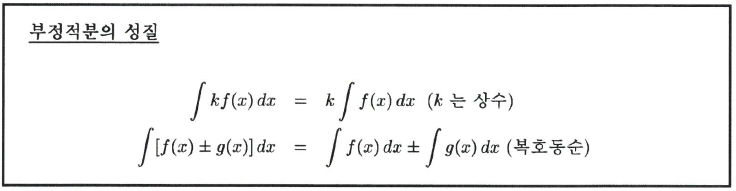
합성함수의 부정적분
함수 $F(x)$가 $f(x)$의 역도함수라고 하자. $f(ax+b)$의 도함수는 $af'(ax+b)$이다. 그렇다면 $f(ax+b)$의 부정적분은 어떻게 될까?
$$[F(ax+b)]'=aF'(ax+b)=af(ax+b)$$
이므로 $f(ax+b)$의 부정적분은
$$\int f(ax+b)dx=\frac{1}{a}F(ax+b)+C$$
가 된다.
치환법칙
일반적인 합성함수의 부정적분을 구하기 위해서는 치환법칙을 많이 사용한다. 치환법칙은 미분에서의 연쇄법칙과 밀접한 관계가 있다. 예를 들어, 다음 부정적분을 구한다고 하자.
$$\int 2x(x^2+1)^2dx$$
$2x(x^2+1)^2=2x^5+4x^3+2x$이므로
$$\begin{align*} \int 2x(x^2+1)^2dx=&\int (2x^5+4x^3+2x)dx \\ =&\frac{1}{3}x^6+x^4+x^2+C \\
=&\frac{1}{3}(x^6+3x^4+3x^2+1)+C'\\=&\frac{1}{3}(x^2+1)^3+C;
\end{align*}$$
을 얻는다. 여기서 $C'=C-\frac{1}{3}$이다. 그러나 연쇄법칙을 이용하여 미분을 구하면
$$(\frac{1}{3}(x^2+1)^3)'=3\frac{1}{3}(x^2+1)^2(x^2+1)'=2x(x^2+1)^2$$
이므로
$$\int 2x(x^2+1)^2dx=\frac{1}{3}(x^2+1)^3+C$$
임을 알 수 있다. 일반적으로 함수 $u=g(x)$가 미분가능하고 함수 $f(u)$의 한 역도함수가 $F(u)$ 일 때, 연쇄법칙에 의하여
$$\begin{align*}
[F(g(x))]'\quad=&\quad F'(g(x))g'(x) \\=&\quad f(g(x))g'(x)
\end{align*}$$
을 얻는다. 즉, $F(g(x))$는 $f(g(x))g'(x)$의 역도함수이다.
$$\int f(g(x))g'(x)dx=F(g(x))+C=F(u)+C$$
이다. $F(u)+C=\int f(u)du$이므로 다음 공식을 얻는다.
$$\int f(g(x))g'(x)dx=F(u)+C=\int f(u)du$$
이렇게 합성함수 $f(g(x))$에서 $g(x)$를 $u$로 치환하여 적분하는 방법을 치환적분법(integration by substitution)이라고 한다.

라이프니츠의 표기법을 이용하면 위 식은 다음과 같이 쓸 수 있다.
$$\int f(g(x))g'(x)dx=\int f(u)\frac{du}{dx}dx=\int f(u)du$$
따라서 $u=g(x)$일 때 $\frac{du}{dx}=g'(x)$를
$$du=g'(x)dx\quad or\quad dx=\frac{1}{g'(x)}du$$
로 나타내기로 한다.
$f'(x)/f(x)$의 적분
$f(x)\neq0$인 분수함수 $\frac{f'(x)}{f(x)}$의 부정적분을 구하여 보자.
$$u=f(x)$$
라고 하면
$$du=f'(x)dx$$
이므로
$$\begin{align*}
\int \frac{f'(x)}{f(x)}dx=&\int \frac{1}{u}du \\=&log\;|u|+C \\=&log\;|f(x)|+C
\end{align*}$$
를 얻는다.
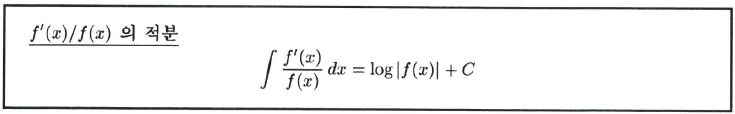
'생활공학 > 대학기초수학' 카테고리의 다른 글
| 6-3 미적분의 기본정리 (0) | 2020.11.26 |
|---|---|
| 6-2 정적분 (0) | 2020.11.26 |
| 5-2 최적화 문제 (0) | 2020.11.25 |
| 5-1 로피탈의 법칙 (0) | 2020.11.25 |
| 4-5 지수,로그함수의 도함수 (0) | 2020.11.25 |




댓글