2절 정적분
수학에서 가장 오래된 문제 중의 하나는 도형의 넓이를 구하는 문제이다. 직사각형의 넓이는 가로와 세로의 곱으로 구할 수 있고 삼각형의 넓이는 밑변과 높이의 곱의 1/2로 구할 수 있다.

일반적인 도형의 경계가 직선인 경우는 삼각형의 넓이를 이용하면 항상 그 넓이를 구할 수 있다. 그러나 경계가 곡선인 경우, 넓이를 구하는 문제는 그리 단순하지가 않다. 이 절에서는 곡선으로 둘러 싸인 도형의 넓이를 구하는 방법을 소개하도록 한다.
곡선 아래 부분의 넓이
함수 $y=x^2,\;\; 0\leq x\leq 1$의 아래 부분 S의 넓이 $A=|S|$를 근사적으로 구하여 보기로 하자.

우선 주어진 영역의 넓이는 높이가 1인 사각형에 포함되므로 0과 1 사이임을 쉽게 알 수 있다. 이제 구간 [0,1]을 네 개로 나누고 각 구간에서의 영역을 각각 $S_1,S_2,S_3,S_4 $ 로 나타내자. 그러면 영역 $ S_i $는 밑변의 길이가 1/4이고 높이가 $(\frac{i}{4})^2$인 직사각형에 포함된다.
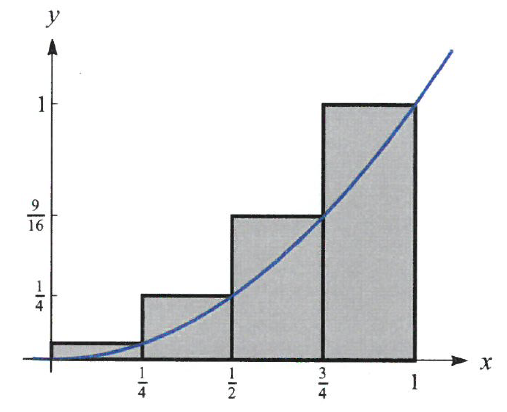
따라서 $S_i$의 넓이 $|S_i|$는 다음 부등식을 만족한다.
$$|S_i|\leq\frac{1}{4}(\frac{i}{4})^2$$
따라서
$$A\leq\frac{1}{4}[(\frac{1}{4})^2+(\frac{2}{4})^2+(\frac{3}{4})^2+(\frac{4}{4})^2]=\frac{15}{32}$$
임을 알 수 있다. 이 식의 오른쪽 값을 구간의 개수가 4인 오른쪽 리만합이라고 하고 $R_4$로 나타낸다. $S_i$를 포함하는 대신 $S_i$에 포함되는 직사각형을 사용하면 반대 방향의 근사값을 구할 수 있다.

즉, 영역 $S_i$는 밑변의 길이가 1/4이고 높이가 $(\frac{i-1}{4})^2$ 인 직사각형을 포함하므로
$$|S_i|\geq\frac{1}{4}(\frac{i-1}{4})^2$$
이다. 따라서
$$A\geq\frac{1}{4}[(\frac{0}{4})^2+(\frac{1}{4})^2+(\frac{2}{4})^2+(\frac{3}{4})^2]=\frac{7}{32}$$
이 성립한다. 이 식의 오른쪽 값을 구간의 개수가 4인 왼쪽 리만합이라고 하고 $L_4$로 나타낸다. 그러므로
$$\frac{7}{32}\leq A \leq\frac{15}{32}$$
가 성립한다. 구간의 갯수를 늘려서 계산하면 좀 더 정확한 $A$의 범위를 구할 수 있다. 예를 들어 구간의 수를 10개로 늘려 계산하면 다음과 같은 $A$의 범위를 얻는다.
$$0.285\leq A\leq 0.385$$
다음 표는 구간의 수 $n$을 늘려가면서 왼쪽 리만합과 오른쪽 리만합을 구한 것이다.
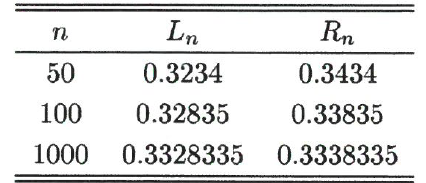
위의 표에 의하면 항상
오른쪽 리만합 - 왼쪽 리만합 = 1/n
이다. 이와 같이 평면도형의 넓이를 구하기 위하여 평면도형을 작은 사각형으로 분할하고, 그 넓이의 합을 구하여 그 극한값을 취하는 방법을 구분구적법이라고 한다. 입체도형의 부피를 구하는 데에도 구분구적법을 사용할 수 있다.
정적분과 넓이
이제 연속함수 $y=f(x)$가 $f(x)\geq0$ 일 때, 곡선 $y=f(x) \geq0$와 $x$축, 그리고 두 수직선 $x=a,x=b$로 둘러 싸인 영역의 넓이를 구하여 보기로 하자. 구간 [a,b]를 $n$등분하여 양끝점과 각 분점의 $x$좌표를
$$x_0(=a),\; x_1, \;x_2, \;\cdots, \;x_{n-1},\; x_n(=b)$$
이라 하고 부분구간의 길이를
$$\delta=x_k-x_{k-1}=\frac{b-a}{n}$$
이라 하자. 구간
$$[x_{k-1}, x_k]=[a+\frac{k-1}{n}(b-a), a+\frac{k}{n}(b-a)]$$
에서 어느 점 $x_k^*$를 잡더라도 다음 직사각형의 합
$$f(x_1^*)\Delta x+\cdots+f(x_n^*)\Delta x=\sum_{k=1}^{n}f(x_n^*)\Delta x $$
는 일정한 값으로 수렴함이 알려져 있다.
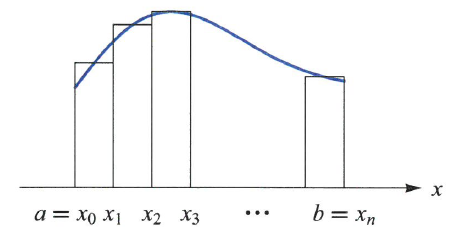
이 극한값을 구간 $[a,b]$에서 함수 $f(x)$의 정적분이라고 하고 $\int_{a}^{b}f(x)dx$로 나타낸다.
$$\int_{a}^{b}f(x)dx=\lim_{n\rightarrow\infty}\sum_{k=1}^{n}f(x_n^*)\Delta x\qquad (6.2)$$
이 경우 $\int_{a}^{b}f(x)dx$가 주어진 영역의 넓이가 됨을 정의로부터 쉽게 이해할 수 있다.

연속함수 $y=f(x)$가 구간 [a,b]에서 $f(x)\geq0$이라고 하자. 그러면
$$\int_{a}^{b}f(x)dx=0$$
이면 $f(x)\equiv 0$이다.
정적분
일반적으로 연속인 함수 $y=f(x)$에 대하여 (6.2)에서 극한값이 존재할 때, 그 극한값을 함수 $f$의 $[a,b]$에서의 리만적분(Riemann integral), 또는 정적분(definite integral)이라 하고
$$\int_{a}^{b}f(x)dx$$
로 나타낸다.

정적분의 성질
$a\leq b$일 때, $\int_{a}^{b}f(x)dx$는 함수 $f(x)$의 구간 [a,b]에서의 정적분으로
$$\sum_{k=1}^{n}f(x_k^*)\Delta x=\sum_{k=1}^{n}f(x_k^*)\frac{b-a}{n}$$
의 극한값으로 정의한다. 정적분 $\int_{b}^{a}f(x)dx$ 도 같은 방법으로 정의한다. 그러나 이 때
$$\Delta x=\frac{a-b}{n}=-\frac{b-a}{n}$$
이므로 리만합은 다음과 같다.
$$\begin{align*}\sum_{k=1}^{n}f(x_k^*)\Delta x =&\sum_{k=1}^{n}f(x_k^*)(-\frac{b-a}{n})\\
=&-\sum_{k=1}^{n}f(x_k^*)\frac{b-a}{n}
\end{align*}$$
따라서 다음 관계식이 성립한다.
$$\int_{b}^{a}f(x)dx=-\int_{a}^{b}f(x)dx$$
만약 $a=b$이면 $\Delta x =0$이므로
$$\int_{a}^{a}f(x)dx=0$$
이다. 정적분의 정의를 이용하여 다음과 같은 정적분의 성질들이 성립함을 보일 수 있다.

$a\leq x \leq b$에서 $f(x)\geq0$이면 정적분 $\int_{a}^{b}f(x)dx$는 곡선 $y=f(x)$와 $x$축, 그리고 두 직선 $x=a$와 $x=b$로 둘러 싸인 영역의 넓이가 된다. 이제 구간 $[a,b]$에서
$$f(x)\leq0$$
일 때 $y=f(x)$와 $x=a, x=b$, 그리고 $y$ 축으로 둘러싸인 영역의 넓이를 $A$ 라고 보자. $-f(x)\geq0$이므로 주어진 영역의 넓이는 $y=-f(x)$와 $x=a, x=b$ 그리고 $x$축으로 둘러싸인 영역의 그것과 같다.

따라서 주어진 영역의 넓이 $A$는
$$A=\int_{a}^{b}(-f(x))dx=-\int_{a}^{b}f(x)dx\qquad\qquad(6.4)$$
가 된다. 다시 말해서
$$\int_{a}^{b}f(x)dx=-A$$
이다.
'생활공학 > 대학기초수학' 카테고리의 다른 글
| 6-4 넓이와 응용 (0) | 2020.11.26 |
|---|---|
| 6-3 미적분의 기본정리 (0) | 2020.11.26 |
| 6-1 부정적분 (0) | 2020.11.26 |
| 5-2 최적화 문제 (0) | 2020.11.25 |
| 5-1 로피탈의 법칙 (0) | 2020.11.25 |




댓글