4절 넓이와 응용
2절에서 양의 함수 $y=f(x)$에 대하여
$$\int_{a}^{b}f(x)dx$$
는 구간 $[a,b]$에서 곡선의 그래프와 $x$ 축 사이 영역의 넓이임을 보았다. 이제 구간 $[a,b]$에서 두 곡선 $y=f(x)$와 $y=g(x)$사이의 영역의 넓이는 어떻게 구할 수 있는 지 알아보기로 한다.
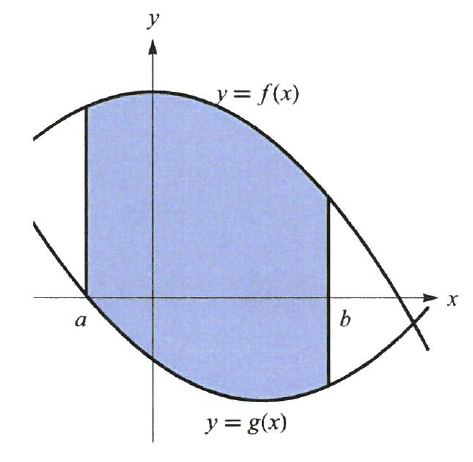
두 함수는 모두 연속이고 $f(x)\geq g(x)$라고 가정한다. 2절에서 한 것과 마찬가지로 구간 $[a,b]$를 $n$ 등분하여 양 끝점과 각 분점의 $x$좌표를
$$x_0(=a),x_1,x_2,\cdots,x_{n-1},x_n(=b)$$
이라 하고 부분구간의 길이를
$$\Delta x=\frac{b-a}{n}$$
이라 하자. 구간 $[x_{k-1},x_k]$의 임의의 점 $x_k^*$에 대하여 리만합
$$\sum_{k=1}^{n}[f(x_n^*)-g(x_n^*)]\Delta x$$
은 주어진 영역 $S$의 넓이 $A$의 근사값이 되며 $n$이 커지면 더 좋은 근사값을 구하여 준다.

따라서 $n\rightarrow\infty$ 일 때, $f,g$가 연속함수이면 이 극한값이 존재하며 그 극한값을 주어진 영역의 넓이로 정의한다.
$$A=\lim_{n\rightarrow\infty}\sum_{k=1}^{n}[f(x_n^*)-g(x_n^*)]\Delta x$$
이 극한값은 정적분으로 정의되므로 다음과 같은 식을 얻는다.

두 곡선으로 둘러싸인 영역의 넓이를 구하기 위해서는 우선 두 곡선의 교점을 구하여야 한다. 두 함수의 대소관계가 구간에 따라 변하는 경우는 구간에 따라 넓이를 구하여 모두 더한다. 즉, 구간별로 두 함수의 대소관계가 달라지는 경우, $f(x)\geq g(x)$인 구간에서는 $f(x)-g(x)$를, $f(x)\leq g(x)$인 구간에서는 $g(x)-f(x)=-(f(x)-g(x))$를 적분한다. 따라서 피적분함수는 다음과 같이 절대값을 이용하여 하나의 함수로 나타낼 수 있다.
$$|f(x)-g(x)|=\left\{\begin{matrix}
f(x)-g(x), & f(x)\geq g(x)\\
-(f(x)-g(x)), & f(x)\leq g(x)
\end{matrix}\right.$$
그러므로 구간 $[a,b]$에서 두 곡선 사이의 넓이는 다음과 같이 구할 수 있다.

y에 대한 적분
함수를 나타낼 때 우리는 일반적으로 $y=f(x)$로 표시한다. 이때 $x$를 독립변수라고 하고 수평축에, $y$를 종속변수라고 하고 수직축에 나타낸다. 그러나 $x$를 항상 독립변수로 간주해야 할 필요는 없다. $x$를 $y$의 함수로 다루는 것이 더 편할 때에는 $y$를 독립변수로 간주해도 된다. 예를 들어, 두 곡선 $x=y^2, x=y+2$와 $y=0,y=2$로 둘러싸인 영역으로 나타낼 수 있다.

따라서 주어진 영역의 넓이는 다음과 같이 구할 수도 있다.
$$\begin{align*} A=&\int_{0}^{2}[(y+2)-y^2]dy=[\frac{1}{2}y^2+2y-\frac{1}{3}y^3]|_0^2\\=&2+4-\frac{8}{3}=\frac{10}{3}
\end{align*}$$
직선운동과 운동거리
수직선 위를 움직이는 물체가 있을 때 시각 t에서 이 물체의 속도가 $v(t)$, 위치를 $s(t)$라고 하자.
$$v(t)=s'(t)$$
이므로
$$s(t)=\int v(t)dt$$
이다. 따라서 시각 $t_1$에서 시각 $t_2$까지 위치의 변화는
$$s(t_2)-s(t_1)=\int_{t_1}^{t_2}v(t)dt$$
로 나타낼 수 있다. 또한 이 물체가 움직인 거리는
$$d(t)=\int |v(t)|dt$$
가 됨을 알 수 있다.
함수의 평균
유한 개의 수 $y_1,y_2,\cdots,y_n$의 평균 $\bar{y}$는 다음과 같이 정의한다.
$$\bar{y}=\frac{y_1+y_2+\cdots+y_n}{n}$$
그렇다면 연속인 구간에서 함수의 평균은 어떻게 정의할까? 만약 $a\leq x \leq b$에서 $y=f(x)\geq 0$이라면 그래프와 $x$축 사이의 영역의 넓이는
$$A=\int_{a}^{b}f(x)dx$$
이다. $A$는 또한 밑변이 $(b-a)$이고 높이가 $\frac{A}{b-a}$인 직사각형의 넓이이기도 하다. 여기서 $\frac{A}{b-a}$을 구간 $[a,b]$에서 함수 $y=f(x)$의 평균(average)으로 정의한다.
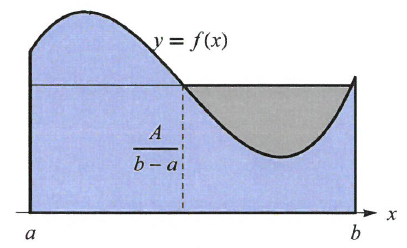
일반적인 연속함수 $y=f(x)$의 평균도 같은 방법으로 정의한다.

정적분의 평균값정리
$F(x)=\int_{a}^{x}f(t)dt$라고 하면 $y=F(x)$는 미분가능한 함수이다. 따라서 평균값정리에 의하면
$$\frac{F(b)-F(a)}{b-a}=F'(c)$$
인 $c$가 $a$와 $b$사이에 존재한다. 그런데 $F'(c)=f(c)$이므로 이 결과는 다음과 같이 쓸 수 있다.
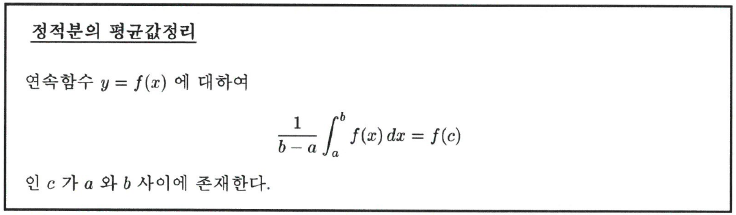
이 결과를 연속함수 $y=f(x)$의 평균 $\bar{f}$와 연결하면
$$\bar{f}=f(c)$$
인 $c$가 $a$와 $b$사이에 존재하는 것을 알 수 있다.
'생활공학 > 대학기초수학' 카테고리의 다른 글
| 7-2 부분적분법 / 7-3 특이적분 (0) | 2020.11.27 |
|---|---|
| 7-1 치환적분 (0) | 2020.11.27 |
| 6-3 미적분의 기본정리 (0) | 2020.11.26 |
| 6-2 정적분 (0) | 2020.11.26 |
| 6-1 부정적분 (0) | 2020.11.26 |




댓글