7-5 곡선의 길이와 곡면의 넓이

5절 곡선의 길이와 곡면의 넓이

함수의 그래프로 만들어지는 영역의 넓이는 직사각형을 이용하여 구하였다. 함수의 그래프의 길이는 직선을 이용하여 근사적으로 구한다.

구간 $[a,b]$를 $n$등분하여

$$x_a=0,x_1=a+\mathrm{\Delta }x,x_{n-1}=a+(n-1)\mathrm{\Delta }x,x_n=b$$

라고 하자. 여기서 $\mathrm{\Delta }x=\frac{b-a}{n}$이다. $x=x_i$에 대응하는 곡선 위의 점을 $P_i=(x_i,f(x_i))$라고 하자.

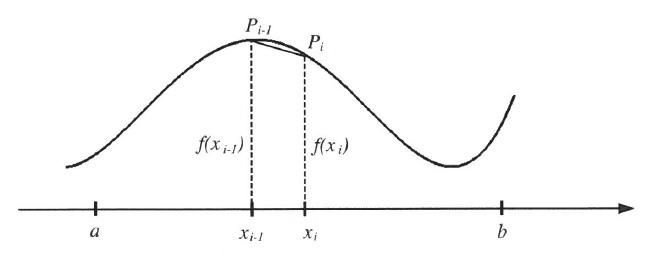
$P_0,P_1,\cdots ,P_n$을 연결하여 얻어진 곡선의 길이는 $y=f(x),a\le x\le b$의 길이의 근사값으로 사용할 수 있으며 그 극한값을 곡선의 길이로 정의한다.

$$L=\underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^n|P_{i-1}{P}_i|$$

여기서 $i$ 번째 구간의 선분 $P_{i-1}{P}_i$의 길이는 

$$|P_{i-1}{P}_i|=\sqrt{(x_i-x_{i-1}{)}^2+(f(x_i)-f(x_{i-1}){)}^2}$$

이다. $f$가 미분가능한 함수라면 평균값 정리에 의하여

$$f(x_i)-f(x_{i-1})=f^{\prime }(x_i^{\ast })(x_i-x_{i-1})=f^{\prime }(x_i^{\ast })\mathrm{\Delta }x$$

을 만족하는 값 $x_i^{\ast }\in [x_{i-1},x_i]$가 존재한다. 따라서

$$|P_{i-1}{P}_i|=\sqrt{1+[f^{\prime }(x_i^{\ast }){]}^2}\mathrm{\Delta }x$$

이므로 $f^{\prime }$이 연속이라면

$$L=\underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^n|P_{i-1}{P}_i|={\int }_a^b\sqrt{1+(f^{\prime }(x){)}^2}dx$$

을 얻는다.

곡선의 길이

같은 방법으로 곡선 $x=g(y),c\le y\le d$ 의 길이는 다음과 같이 구할 수 있다.

$$L={\int }_c^d\sqrt{1+(g^{\prime }(y){)}^2}dy$$

월뿔대의 겉넓이

반지름이 $r$이고 높이가 $h$인 원기둥의 옆넓이는 전개도에서 구할 수 있다. 즉, 옆넓이는 가로 $2\pi r$, 높이 $h$인 직사각형의 넓이이므로

$$A=2\pi rh$$

이다. 원뿔의 옆넓이도 전개도에서 구할 수 있다. 반지름이 $r$이고 모선의 길이가 $l$인 원뿔의 전개도는 반지름이 $l$이고 호의 길이가 $2\pi r$인 부채꼴이다.

원뿔의 전개도

따라서 옆넓이는 

$$A=\pi rl$$

이다. 그렇다면 좀 더 일반적인 회전체의 겉넓이는 어떻게 구할까? 우선 직선의 일부를 $x$축 주위로 회전한 회전체의 겉넓이를 구하여 보자.

원점을 지나는 직선을 $x$축 주위로 회전하면 원뿔이 되지만 원점을 지나지 않는 직선의 경우는 원뿔대가 된다. 반지름 $r_1,r_2(r_1<r_2)$ 인 원뿔대의 옆넓이 $A$는 다음과 같이 원뿔의 옆넓이에서 구할 수 있다.

$$A=\pi r_2(l+\mathrm{\Delta }l)-\pi r_{1}l=\pi [(r_2-r_1)l+r_2\mathrm{\Delta }l](7.5)$$

원뿔대

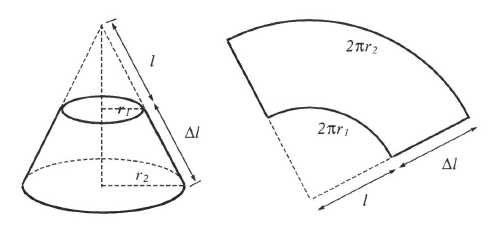
월뿔대에 그린 두 직각삼각형은 닮은 꼴이므로

$$\frac{l}{r_1}=\frac{l+\mathrm{\Delta }l}{r_2}$$

이다. 따라서

$$r_2l=r_1{l+\Delta l)\quad or\quad (r_2-r_1)l=r_1\Delta l$$

이고 이 식을 식 (7.5)에 대입하면

$$A=\pi (r_1+r_2)\mathrm{\Delta }l(7.6)$$

을 얻는다.

회전체의 겉넓이

원기둥이나 원뿔의 경우처럼 전개도를 그릴 수 있다면 입체도형의 겉넓이를 구하는 문제는 평면도형의 넓이를 구하는 문제가 된다. 그러나 일반적인 입체도형의 경우 전개도를 그리는 것은 불가능하다. 그렇다면 회전체의 겉넓이는 어떻게 정의하고 어떻게 구할까? 곡선을 회전시켜 얻어지는 회전체의 겉넓이는 곡선의 길이를 구할 때와 마찬가지로 곡선을 직선으로 근사시켜서 그 회전체의 겉넓이의 극한값으로 정의한다.

미분가능한 함수 $y=f(x)$를 구간 $[a,b]$ 에서 $x$ 축 주위로 회전한 회전체의 겉넓이는 다음과 같이 정의한다. 곡선의 길이를 구할 때와 마찬가지로 구간 $[a,b]$를 $n$ 등분하여

$$x_0=a,a_1=a+\mathrm{\Delta }x,x_{n-1}=a+(n-1)\mathrm{\Delta }x,x_n=b$$

라고 하고 $x=x_i$ 에 대응하는 곡선 위의 점을 $P_i=(x_i,f(x_i))$라고 하자. 여기서 $P_0,P_1,\cdots ,P_n$을 연결하여 얻어지는 곡선을 회전하여 얻어지는 곡면의 넓이를 $S_n$ 이라고 하면 회전체의 겉넓이는 $\underset{n\to \mathrm{\infty }}{lim}{S}_n$ 으로 정의한다. 선분 $P_{i-1}{P}_i$를 $x$ 축 주위로 회전한 회전체는 반지름이 각각 $f(x_{i-1}),f(x_i)$ 이고 옆선의 길이가

$$|P_{i-1}{P}_i|=\sqrt{1+[f^{\prime }(x_i^{\ast }){]}^2}\mathrm{\Delta }x,x_i^{\ast }\in [x_{i-1},x_i]$$

인 원뿔대이다.

회전체 겉넓이

따라서 $i$ 번째 부분곡면의 넓이는 식 (7.6) 으로부터

$$\pi (f(x_{i-1})+f(x_i))|P_{i-1}{P}_i|=\pi (f(x_{i-1})+f(x_i))\sqrt{1+[f^{\prime }(x_i^{\ast }){]}^2}\mathrm{\Delta }x$$

임을 알 수 있다. 따라서 회전체의 겉넓이는 다음과 같이 구할 수 있다.

$$\begin{array}{rl}S=\underset{n\to \mathrm{\infty }}{lim}{S}_n=& \underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^n\pi (f(x_{i-1})+f(x_i))\sqrt{1+[f^{\prime }(x_i^{\ast }){]}^2}\mathrm{\Delta }x\\ =& {\int }_a^{b}2\pi f(x)\sqrt{1+[f^{\prime }(x){]}^2}dx\end{array}$$

이 식을 길이함수 $s(t)={\int }_a^t\sqrt{1+[f^{\prime }(x){]}^2}dx$ 를 이용하면, 즉,

$$ds=\sqrt{1+(f^{\prime }(x){)}^2}dx$$

을 이용하면 다음과 같이 나타낼 수 있다.

$$S={\int }_a^{b}2\pi f(x)ds$$

x축 회전한 회전체의 겉넓이

같은 방법으로 $y$축 주위로 회전한 회전체의 겉넓이는 다음과 같이 구할 수 있다.

y축 회전한 회전체의 겉넓이

도형의 중심

$a\le x\le b$에 대하여 $0\le g(x)\le f(x)$라고 하자. 두 곡선 $y=f(x),y=g(x)$와 두 직선 $x=a,x=b$으로 둘러싸인 영역을 $R$이라고 하자. 이 영역의 중심, 또는 도심(centroid)을 $(\overline{x},\overline{y})$로 나타내고 다음과 같이 정의한다.

$$\begin{gathered} \overline{x}=\frac{1}{A}{\int }_a^{b}x(f(x)-g(x))dx(=\frac{1}{A}{\int }_a^b{\int }_{g(x)}^{f(x)}xdydx) \\ \overline{y}=\frac{1}{A}{\int }_a^b(f^2(x)-g^2(x))dx(=\frac{1}{A}{\int }_a^b{\int }_{g(x)}^{f(x)}ydydx) \end{gathered}$$

여기서 $A={\int }_a^b[f(x)-g(x)]dx$ 는 영역 $R$의 넓이이다.

부피에 대한 파푸스의 정리

곡선 $y=f(x),a\le x\le b(a>0)$을 $y$축 주위로 회전한 회전체의 부피는

$$V={\int }_a^{b}2\pi xf(x)dx$$

이다. 다시 두 곡선 $y=f(x),y=g(x)$와 $x=a,x=b$로 둘러싸인 영역을 $R$이라고 하자. 여기서 $g(x)\le f(x)$라고 가정한다. 영역 $R$을 $y$축 둘레로 회전시킨 회전체의 부피 $V$는 

$$\begin{array}{rl}V=& 2\pi {\int }_a^{b}x(f(x)-g(x))dx\\ =& 2\pi \overline{x}\cdot A\end{array}$$

가 된다. 다시 말해서, 회전체의 부피 $V$는 영역의 중심의 $x$좌표 $\overline{x}$ 가 반지름인 원의 둘레 $2\pi \overline{x}$에 영역 $R$의 넓이 $A$를 곱한 것이다. 마찬가지로 $f(x)\ge g(x)\ge 0$일 때 영역 $R$을 $x$ 축 둘레로 회전한 회전체의 부피는

$$\begin{array}{rl}V=& \pi {\int }_a^b[(f^2(x)-g^2(x)]dx\\ =& 2\pi \overline{y}\cdot A\end{array}$$

이다. 즉, $x$ 축 둘레로 회전한 회전체의 부피 $V$는 영역 $R$의 중심의 $y$좌표 $\overline{y}$를 반지름으로 하는 원의 길이 $2\pi \overline{y}$에 영역 $R$의 넓이 $A$를 곱한 것이다. 이 결과는 3세기경 그리스의 수학자 파푸스의 이름을 따서 파푸스의 정리(Pappus's Theorem for Volume)라고 부른다.

파푸스의 정리1

곡선의 중심

곡선 $y=f(x),a\le x\le b$에 대하여 다음 식을 만족하는 점 $(\overline{x},\overline{y})$ 을 곡선의 중심(centroid)이라고 한다.

$${\int }_a^b(x-\overline{x})\sqrt{1+[f^{\prime }(x){]}^2}dx=0,{\int }_a^b(f(x)-\overline{y})\sqrt{1+[f^{\prime }(x){]}^2}dx=0$$

곡선의 길이를

$$L={\int }_a^b\sqrt{1+[f^{\prime }(x){]}^2}dx$$

이라고 하면 곡선의 중심은 다음과 같이 구할 수 있다.

$$\begin{gathered} \overline{x}=\frac{1}{L}{\int }_a^{b}x\sqrt{1+[f^{\prime }(x){]}^2}dx \\ \overline{y}=\frac{1}{L}{\int }_a^{b}f(x)\sqrt{1+[f^{\prime }(x){]}^2}dx \end{gathered}$$

곡선의 중심은 일반적으로 곡선 위의 점이 아니다.

겉넓이에 대한 파푸스의 정리

곡선 $y=f(x),a\le x\le b$을 $x$ 축 둘레로 회전한 회전체의 겉넓이 $S$는

$$S=2\pi {\int }_a^{b}f(x)\sqrt{1+[f^{\prime }(x){]}^2}dx$$

이므로

$$S=2\pi \overline{y}\cdot L$$

이다. 다시 말해서, 회전체의 겉넓이 $S$는 곡선의 중심의 $y$좌표 $\overline{y}$을 반지름으로 하는 원의 길이 $2\pi \overline{y}$에 곡선의 길이 $L$을 곱한 것이다. 마찬가지로 $y=f(x)$가 일대일함수일 때, 이 곡선을 $y$축 둘레로 회전한 회전체의 겉넓이 $S$는

$$S=2\pi {\int }_a^{b}x\sqrt{1+[f^{\prime }(x){]}^2}dx$$

가 됨을 보일 수 있다. 따라서

$$S=2\pi \overline{x}\cdot L$$

이다. 다시 말해서, 회전체의 겉넓이 $S$는 곡선의 중심의 $x$ 좌표 $\overline{x}$을 반지름으로 하는 원의 길이 $2\pi \overline{x}$ 에 곡선의 길이 $L$을 곱한 것이다. 이 결과도 파푸스의 정리라고 부른다.

파푸스의 정리2