1절 평균변화율과 순간변화율
이 세상의 대부분의 것은 시간이 흐르면 변한다. 이러한 변화는 변화율을 사용하여 수학적으로 나타낼 수 있는데 변화율은 변화가 어느 방향으로 얼마나 빠르게 일어나는지를 나타낸다. 변화가 시간에 관계없이 일정하게 일어나면 직선의 형태로 나타낼 수 있고, 이때 직선의 기울기는 변화율을 나타낸다. 이 경우, 변화율은 시간에 상관없이 항상 일정하다. 그러나 대부분의 경우 변화율은 시간에 따라 다르게 나타나는데 이 절에서는 이러한 변화율에 관한 체계적이고 직접적인 방법을 살펴보기로 한다.
보간법
자연현상, 또는 사회현에서 관찰되는 변화나 실험실에서 측정되는 변화는 시간에 대하여 연속적으로 기록하는 것이 불가능하다. 따라서 일정한 시간간격을 두고 이러한 수치를 관측하여 기록한다. 그렇다면 관측되지 않은 시점에서의 값은 어떻게 추정할까? 여러가지 방법 중에서 가장 일반적으로 사용하는 방법은 보간법이다.
다음표는 어느 하루의 기온을 한 시간마다 기록한 것이다.

이렇게 몇 개의 시점에서만 관측된 경우 관측되지 않은 시점에서의 값은 일반적으로 이웃한 두 점을 직선으로 연결하여 나타낸다. 이렇게 함수를 나타내는 방법을 보간법(interpolation)이라고 한다.
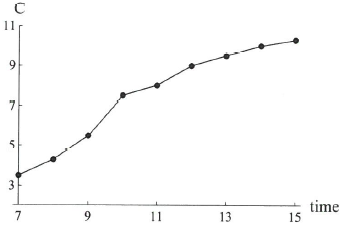
이때 두 점을 연결한 직선의 기울기를 두 점 사이의 평균변화율(average rate of change)이라고 한다. 다시 말해서, $f(t)$를 $t$시에서의 기온이라고 한다면 두 점 $(t_1,f(t_1)), (t_2,f(t_2)) $사이의 평균변화율은
$$\frac{f(t_2)-f(t_1)}{t_2-t_1}$$
으로 정의한다.
평균변화율
함수 $y=f(x)$가 $a$를 포함하는 열린 구간에서 정의되었다고 하자. 변수 $x$가 $a$에서 $a+h$로 변할 때, $x$의 변화량을
$$\Delta x=h$$
로 나타내고 그에 대응하는 종속변수 $y$의 변화량을
$$\Delta y=f(a+h)-f(a)$$
로 나타내자. 여기에서 $y$의 변화량을 $x$의 변화량으로 나눈 몫
$$\frac{\Delta y}{\Delta x}=\frac{f(a+h)-f(a)}{h}$$
을 구간 $[a,a+h]$에서 $x$에 대한 $f$의 평균변화율(average rate of change)이라 한다. 이 평균변화율은 다음 그림에서 직선 $PQ$의 기울기이다.

수직선 위를 움직이는 물체가 있다고 하자. 시간 $t$에서 이 물체의 위치를 $s(t)$라고 하면 시각 $t$에서 시각 $t+h$까지의 평균속도(average velocity)는 위치의 변화를 시간으로 나눈 것이다.
$$\frac{\Delta s}{\Delta t}=\frac{s(t+h)-s(t)}{h}$$
순간변화율
평균속도를 점점 짧은 시간에서 구하면 즉, $h\rightarrow0$일 때 이 값을 순간속도로 정의한다. 또는 단순히 속도(velocity)로 정의한다. 다시 말해서 시각 $t$에서의 속도 $v(t)$는
$$v(t)=\lim_{h\rightarrow0}\frac{s(t+h)-s(t)}{h}$$
으로 정의한다. 여기서 $s(t)$는 물체의 위치를 나타내므로 $v(t)>0$이면 양의 방향으로, $v(t)<0$이면 음의 방향으로 움직임을 의미한다. 속도의 절대값 $|v(t)|$를 속력(speed)이라고 한다.
일반적으로 함수 $y=f(x)$에 대하여 $\Delta x=h$가 0에 가까워짐에 따라 평균변화율
$$\frac{\Delta y}{\Delta x}=\frac{f(a+h)-f(a)}{h}$$
가 어떤 값에 수렴하면 이 값을 $x=a$에서의 순간변화율, 또는 $x=a$에서의 미분계수(derivative)라고 하고
$$f'(a),\quad or\quad y'\mid _{x=a}$$
로 나타낸다. 극한값 $f'(a)$가 존재할 때 함수 $f$는 $x=a$에서 미분가능하다(differentiable)고 한다. $x=a+h$라고 하면 $h\rightarrow0$일 때 $x\rightarrow a$이므로
$$f'(a)=\lim_{h\rightarrow0}\frac{f(a+h)-f(a)}{h}=\lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a}$$
으로 나타내기도 한다.

미분가능한 함수는 연속이다.
$f$가 $x=a$에서 미분가능하다고 하자. 그러면
$$f(x)-f(a)=\frac{f(x)-f(a)}{x-a}(x-a)$$
에서 다음 두 극한값이 존재한다.
$$\lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a}=f'(a),\quad \lim_{x\rightarrow a}(x-a)=0$$
따라서
$$\lim_{x\rightarrow a}(f(x)-f(a))=f'(a)\cdot0=0$$
또는
$$\lim_{x\rightarrow a}f(x)=f(a)$$
이 성립한다. 그러므로 $f$는 $x=a$에서 연속이다. 그리고 대우명제를 생각하면
"함수 $f$가 $x=a$에서 연속이 아니면 미분가능하지 않다."
는 것을 알 수 있다. 그러나 그 역은 참이 아니다. 다시 말해서 $f$가 $x=a$에서 연속이라고 해서 항상 미분가능한 것은 아니다.
$h>0$이면서 0으로 갈 때 우극한
$$\lim_{h\rightarrow0^+}\frac{f(a+h)-f(a)}{h}$$
가 존재하면 그 값을 $f'_+(a)$로 나타내고 $x=a$에서 $f$의 우미분계수(right-hand derivative)라고 한다. 마찬가지로, $h<0$이면서 0으로 갈 때 좌극한
$$\lim_{h\rightarrow0^-}\frac{f(a+h)-f(a)}{h}=-\lim_{h\rightarrow0^+}\frac{f(a+h)-f(a)}{h}$$
가 존재하면 그 값을 $f'_-(a)$로 나타내고 $x=a$에서 $f$의 좌미분계수(left-hand derivative)라고 한다. 극한의 성질로부터 우미분계수 $f'_+(a)$와 좌미분계수 $f'_-(a)$ 가 존재하고 두 값이 같으면 $f$는 $x=a$에서 미분가능하고, 이때
$$f'(a)=f'_+(a)=f'_-(a)$$
이다.

국소적 선형성
유클리드에 따르면 원의 접선(tangent line)은 원과 한 점에서 만나는 직선이다.
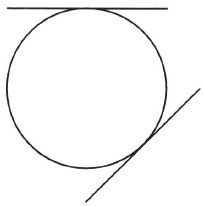
그렇다면 일반적인 그래프에 대하여 접선은 어떻게 정의할까? 원과 접선을 접점 근방에서 확대해 보면 원과 접선이 아주 비슷해 보인다. 일반적으로 $f'(a)$가 존재할 때 곡선 $y=f(x)$의 그래프를 점 $P(a,f(a))$근방에서 확대하면 할수록 곡선은 직선처럼 보인다. 이런 경우 곡선 $y=f(x)$는 $x=a$에서 국소적으로 선형(locally linear)이라 한다.
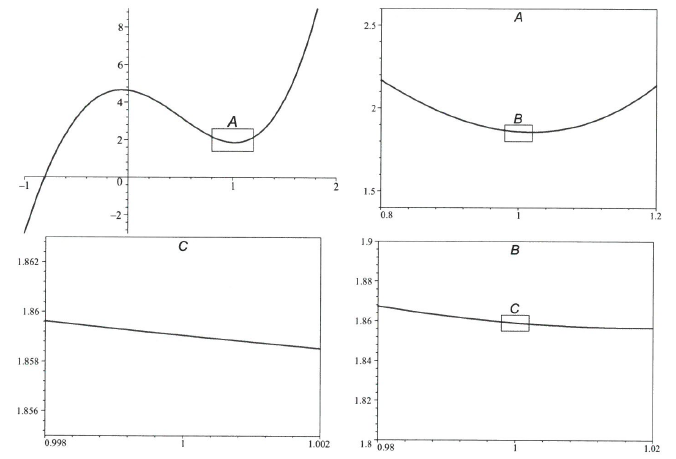
그래프를 확대하면 할수록 곡선 $y=f(x)$ 위의 한 점 $P(a,f(a))$ 근방에서의 평균변화율
$$\frac{f(a+h)-f(a)}{h}$$
는 미분계수 $f'(a)$로 수렴한다. 따라서 미분계수 $f'(a)$를 그 점에서 곡선의 기울기(slope of curve)로 정의하고, 점 $P(a,f(a))$에서 곡선의 기울기와 같은 기울기를 갖는 직선을 접선(tangent line)으로 정의하기로 한다.

일반적으로 국소적 선형성과 미분가능성은 동치이다.

'생활공학 > 대학기초수학' 카테고리의 다른 글
| 3-3 연쇄법칙과 역함수 정리 (0) | 2020.11.20 |
|---|---|
| 3-2 도함수 (0) | 2020.11.20 |
| 2-5 연속함수 (0) | 2020.11.20 |
| 2-4 극한의 계산 (0) | 2020.11.19 |
| 2-3 함수의 극한 (0) | 2020.11.19 |




댓글