1절 삼각함수
각의 크기는 30˚,45˚처럼 일반적으로 60분법을 이용하여 나타낸다. 그러나 이론적으로는 호도법을 이용하여 각의 크기를 실수로 나타낸다. 호도법은 각의 크기를 단위원에서 대응하는 호의 길이를 이용하여 나타내는 방법이다. 단위원에서 호의 길이가 1일 때 대응하는 중심각을 1rad 라고 정의하고 1 라디안(radian)이라고 읽는다.

반지름이 1인 반원의 호의 길이는 $\pi$이므로
$$180^{\circ}=\pi (rad)$$
이다. 따라서
$$30^{\circ}=\frac{180^{\circ}}{6}=\frac{\pi}{6}(rad),\quad 45^{\circ}=\frac{180^{\circ}}{4}=\frac{\pi}{4}(rad)$$
이다. 특별히 혼란의 위험이 없으면 호도법의 단위 rad은 생략하고 사용한다.
삼각함수의 정의
좌표평면에서 원점을 중심으로 하는 단위원은 다음과 같이 음함수를 이용하여 나타낼 수 있다.
$$x^2+y^2=1$$
이때 $x$축에서 양의 방향으로 중심각$\theta$(rad) 에 대응하는 단위원의 좌표를
$$(cos\theta, sin\theta)$$
로 정의한다.

정의에 의하면 점 $(cos\theta, sin\theta)$ 는 모든 실수 $\theta$에 대하여 단위원 위에 있으므로 다음식이 성립한다.
$$cos^2\theta+sin^2\theta=1$$
단위원의 중심각은 $2\pi$이므로 코사인 함수 cos와 사인함수 sin은 모두 주기가 $2\pi$인 주기함수이다.
$$cos(\theta+2k\pi)=cos\theta,\qquad sin(\theta+2k\pi)=sin\theta$$

또한 원의 대칭성에 의하여 다음 등식들이 성립함을 알 수 있다.
$$cos(-\theta)=cos\theta,\quad sin(-\theta)=-sin\theta\\
cos((\pi-\theta)=-cos\theta,\quad sin(\pi-\theta)=sin\theta\\
cos(\pi+\theta)=-cos\theta,\quad sin(\pi+\theta)=-sin\theta$$
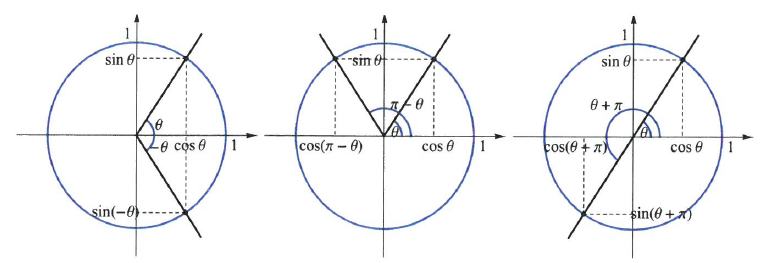

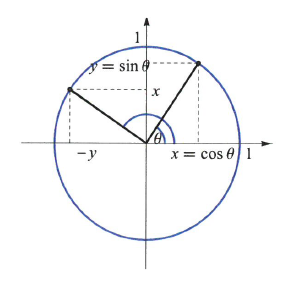
단위원 위의 점 $(x,y)$를 양의 방향으로 $\pi/2(=90^{\circ})$ 만큼 회전하면 $(-y,x)$가 되므로
$$cos(\theta+\frac{\pi}{2})=-sin\theta,\quad sin(\theta+\frac{\pi}{2})=cos\theta\qquad(4.1)$$
가 성립한다.
식(4.1)과 삼각함수의 성질2의 첫 번째 식을 이용하면
$$cos(\frac{\pi}{2}-\theta)=-sin(-\theta)=sin\theta\\sin(\frac{\pi}{2}-\theta)=cos(-\theta)=cos\theta$$
임을 알 수 있다.

탄젠트함수 tan는
$$tan\theta=\frac{sin\theta}{cos\theta}$$
로 정의한다. $\theta=n\pi+\frac{\pi}{2}$에서만 $cos\theta=0$이므로 탄젠트함수의 정의역은 $\theta\neq n\pi+\frac{\pi}{2}$인 실수이다. 사인과 코사인의 대한 성질을 이용하면 다음 식이 성립함을 알 수 있다.
$$tan(-\theta)=-tan\theta \\ tan(\pi-\theta)=-tan\theta \\ tan(\pi+\theta)=tan\theta$$
마지막 식에서 코사인함수, 사인함수와는 달리 탄젠트함수의 주기는 $\pi$임을 알 수 있다.
삼각함수의 덧셈정리
단위원 위의 두 점 A(1,0)과 B($cos(\alpha+\beta), sin(\alpha+\beta)$)사이의 거리는 두 점 C$(cos\alpha, sin\alpha)$와 D$(cos(-\beta), sin(-\beta))=(cos\beta, -sin\beta)$ 사이의 거리와 같다.

따라서
$$(1-cos(\alpha+\beta))^2+sin^2(\alpha+\beta)=(cos\alpha-cos\beta)^2+(sin\alpha+sin\beta)^2$$
이 성립한다. 항등식 $cos^2\theta+sin^2\theta=1$을 이용하여 이 식을 정리하면
$$2-2cos(\alpha+\beta)=2-2(cos\alpha cos\beta - sin\alpha sin\beta)$$
이 되므로
$$cos(\alpha+\beta)=cos\alpha cos\beta-sin\alpha sin\beta$$
을 얻는다. 이 식에 $\beta$대신 $-\beta$를 대입하면
$$cos(\alpha-\beta)=cos\alpha cos\beta+sin\alpha sin\beta$$
이 성립하고 이 식에서 $\alpha$대신 $\frac{\pi}{2}-\alpha$을 대입하면
$$\begin{align*}sin(\alpha+\beta)=& cos(\frac{\pi}{2}-\alpha-\beta)\\
=&cos(\frac{\pi}{2}-\alpha)cos\beta+sin(\frac{\pi}{2}-\alpha)sin\beta\\
=&sin\alpha cos\beta+cos\alpha sin\beta \end{align*}$$
를 얻는다. 마지막으로 이 식의 $\beta$대신 $-\beta$를 대입하면
$$sin(\alpha-\beta)=sin\alpha cos\beta - cos\alpha sin\beta$$
를 얻는다. 또한 탄젠트함수의 정의에 의하여
$$tan(\alpha+\beta)=\frac{sin(\alpha+\beta)}{cos(\alpha+\beta)}=\frac{sin\alpha cos\beta+cos\alpha sin\beta}{cos\alpha cos\beta-sin\alpha sin\beta}$$
이 성립한다. 분자와 분모를 모두 $cos\alpha cos\beta$로 나누면
$$tan(\alpha+\beta)=\frac{tan\alpha+tan\beta}{1-tan\alpha tan\beta}$$
를 얻는다. 이 식에 $\beta$ 대신 $-\beta$를 대입하면
$$tan(\alpha-\beta)=\frac{tan\alpha-tan\beta}{1+tan\alpha tan\beta}$$
을 얻는다. 위에 얻은 여러가지 등식을 삼각함수의 덧셈정리라고 한다.

삼각함수의 배각공식
코사인함의 덧셈정리에서 $\alpha=\beta=0$이면
$$\begin{align*} cos(2\theta)=&cos\theta cos\theta-sin\theta sin\theta\\=&cos^2\theta-sin^2\theta\\=&2cos^2\theta-1=1-2sin^2\theta\end{align*}$$
을 얻는다. 같은 경우 사인함수와 탄젠트함수에 대한 관계식도 정리하면 다음과 같다. 이 등식을 배각공식이라고 한다.

코사인에 대한 배각공식은 다음과 같이 바꾸어 쓸 수 있다.
$$cos^2\theta=\frac{1+cos2\theta}{2},\qquad sin^2\theta=\frac{1-cos2\theta}{2}$$
따라서
$$tan^2\theta=\frac{1-cos2\theta}{1+cos2\theta}$$
을 얻는다. 이 식들에 $\theta$ 대신 $\theta/2$를 넣은 것을 반각공식이라고 한다.

삼각함수의 합성
실수 a,b에 대하여
$$y=f(x)=asinx+bcosx$$
는 주기가 $2\pi$인 주기함수이다. 이제 이 함수의 최대값을 구해보기로 한다. $A=\sqrt{a^2+b^2}$라고 하면
$$acosx+bsinx=A[\frac{a}{A}cosx+\frac{b}{A}sinx]$$
이다.
$$(\frac{a}{A})^2+(\frac{b}{A})^2=1$$
이므로 점 $(\frac{a}{A},\frac{b}{A})$는 단위원 $x^2+y^2=1$위의 점이다. 따라서
$$cos\alpha=\frac{a}{A},\quad sin\alpha=\frac{b}{A}$$
인 $\alpha$에 대하여
$$\frac{a}{A}cosx+\frac{b}{A}sinx=cos\alpha cosx+sin\alpha sinx=cos(x-\alpha)$$
이 성립한다. 그러므로
$$f(x)=acosx+bsinx=Acos(x-\alpha)$$
으로 쓸 수 있고 최대값은 $A=\sqrt{a^2+b^2}$, 최소값은 -A이다. $y=f(x)$의 그래프는 $y=Acosx$의 그래프를 x축 양의 방향으로 $\alpha$만큼 평행이동하면 얻어진다.

이렇게 $acosx+bsinx$꼴의 함수를 $Acos(x-\alpha)$, 또는 $Asin(x+\beta)$꼴로 바꾸어 쓸 수 있는데 이를 삼각함수의 합성이라고 한다.

'생활공학 > 대학기초수학' 카테고리의 다른 글
| 4-4 지수함수와 로그함수 (0) | 2020.11.24 |
|---|---|
| 4-2 / 4-3 삼각함수와 역삼각함수의 도함수 (0) | 2020.11.24 |
| 3-5 함수의 그래프 (0) | 2020.11.24 |
| 3-4 평균값 정리와 극값 (0) | 2020.11.23 |
| 3-3 연쇄법칙과 역함수 정리 (0) | 2020.11.20 |




댓글