2-2 급수

수열 ($a_n$)의 각 항을 모두 더한 것을

$$a_1+a_2+a_3+....$$

로 나타내고 무한급수(infinite series), 또는 단순히 급수(series)라고 부른다. 급수를 간단히 다음과 같이 나타내기도 한다.

$$\sum _{n=1}^{\mathrm{\infty }}{a}_n,or\sum a_n$$

부분합

다음과 같이 정의된 수열 ($s_n$)을 무한급수 $\sum a_n$의 부분합(partial sum)의 수열이라고 한다.

$$\begin{array}{rl}{s}_1=& a_1\\ s_2=& a_1+a_2\\ & ⋮\\ s_n=& a_1+a_2+\cdots +a_n=\sum _{k=1}^n{a}_k\\ & ⋮\end{array}$$

부분합의 수열 ($s_n$)이 극한값 s로 수렴하면 무한급수는 수렴한다고 하고 s를 무한급수의 합(sum of series)이라고 부른다. 즉, 

$$\begin{array}{rl}s=& \underset{n\to \mathrm{\infty }}{lim}{s}_n=\underset{n\to \mathrm{\infty }}{lim}\sum _{k=1}^n{a}_k=\sum _{n=1}^{\mathrm{\infty }}{a}_n\\ =& a_1+a_2+\cdots +a_n+\cdots \end{array}$$

($s_n$)이 발산하면 무한급수도 발산한다고 한다. 

등비급수

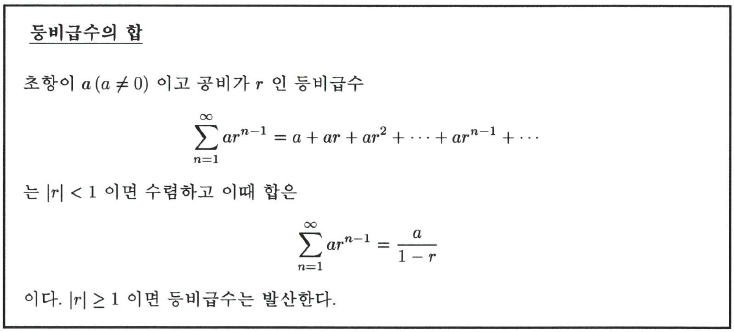
무한급수 중 가장 중요한 등비급수 또는 기하급수(geometric series)이다. 초항이 $a(\ne 0)$이고 공비가 r인 등비급수는 다음과 같이 정의된다.

$$a+ar+a{r}^2+\cdots +a{r}^{n-1}+\cdots =\sum _{n=1}^{n}a{r}^{n-1}$$

r=1이면 부분합은 $n\to \mathrm{\infty }$일 때,

$$s_n=a+a+\cdots +a=na\to \{\begin{array}{cc}\mathrm{\infty },& a>0\\ -\mathrm{\infty },& a<0\end{array}$$

이므로 등비급수는 발산한다. 한편 $r\ne 1$이면

$$\begin{array}{rl}{s}_n=& a+ar+a{r}^2+\cdots +a{r}^{n-1}\\ r{s}_n=& ar+a{r}^2+\cdots +a{r}^{n-1}+a{r}_n\end{array}$$

에서

$$s_n-r{s}_n=a-a{r}^n\Rightarrow s_n=\frac{a(1-r^n)}{1-r}$$

이다. $-1<r<1$이면 $r^n\to 0$이므로$(n\to \mathrm{\infty })$

$$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{lim}{s}_n=& \underset{n\to \mathrm{\infty }}{lim}\frac{a(1-r^n)}{1-r}\\ =& \frac{a}{1-r}-\frac{a}{1-r}\underset{n\to \mathrm{\infty }}{lim}{r}^n=\frac{a}{1-r}\end{array}$$

이다. $r>1$이거나 $r\le -1$이면 $r^n$은 발산하므로 등비급수도 발산한다.

등비급수의 합

순환소수

순환하는 무한소수는 무한급수의 합으로 쓸 수 있다. 예를 들어

$$\begin{array}{rl}0.\dot{3}=& 0.3333\cdots =0.3+0.03+0.003+\cdots \\ =& \sum _{n=1}^{\mathrm{\infty }}0.3(0.1{)}^{n-1}\\ 1.1\dot{2}\dot{1}=& 1.1+0.021+0.00021+\cdots \\ =& 1.1+\sum _{n=1}^{\mathrm{\infty }}0.021(0.01{)}^{n-1}\end{array}$$

따라서 순환하는 무한소수는 항상 분수로 표현할 수 있다.

$$\begin{array}{rl}0.\dot{3}=& \frac{0.3}{1-0.3}=\frac{1}{3}\\ 1.1\dot{2}\dot{1}=& 1.1+\frac{0.021}{1-0.01}=\frac{363}{330}+\frac{7}{330}=\frac{37}{33}\end{array}$$

P진법

각자리 수가 p의 거듭제곱을 나타내는 표시법을 p진법이라 한다. 십진법과 구분하기 위하여 수 밑에 작게 (p)를 적어준다.

P 진법 표시

수렴하는 급수의 기본 성질

무한급수 $\sum _{n=1}^{\mathrm{\infty }}{a}_n$이 s로 수렴한다고 하자. 그러면

$$a_n=s_n-s_{n-1}$$

이므로

$$\underset{n\to \mathrm{\infty }}{lim}{a}_n=\underset{n\to \mathrm{\infty }}{lim}{s}_n-\underset{n\to \mathrm{\infty }}{lim}{s}_{n-1}=s-s=0$$

이다. 따라서 $\underset{n\to \mathrm{\infty }}{lim}{a}_n$이 존재하지 않거나 $\underset{n\to \mathrm{\infty }}{lim}{a}_n\ne 0$이면 $\sum _{n=1}^{\mathrm{\infty }}{a}_n$은 발산한다.

일반항 판정법

무한급수의 합은 수열의 부분합의 극한으로 정의되므로 수열에 대하여 성립한 많은 성질들이 무한급수에 대하여도 성립한다.

수렴하는 급수의 기본 성질