2-1 수열

1절 수열

수를 순서대로 배열한 것을 수열(sequence)이라 부른다. 즉, 수열이란 자연수의 집합

$$\mathbb{N}=\{1,2,3,...\}$$

에서 정의된 함수이다. 예를 들어 수열

$$(1,\frac{1}{2},\frac{1}{3},\frac{1}{4},...)$$

에서 초항은 1, 둘째 항은 1/2이고, n 번째 항은

$$a_n=\frac{1}{n},n\ge 1$$

이다. 이때 $a_n$을 일반항이라고 한다. 수열은 다음과 같이 그래프를 이용하여 나타낼 수도 있다.

수열 그래프

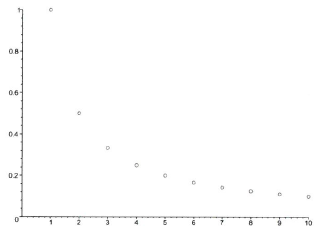
이 그래프에서 $a_n=1/n$은 n이 커질수록 0에 가까워짐을 알 수 있다. 이때 이 수열의 극한값(limit of sequence)은 0 이라고 하고

$$\underset{n\to \mathrm{\infty }}{lim}{a}_n=\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n}=0$$

이라고 표현한다. 일반적으로 n이 커짐에 따라 $a_n$의 값이 L에 가까워질 때 수열 $a_n$은 극한값 L을 갖는다고 하고

$$\underset{n\to \mathrm{\infty }}{lim}{a}_n=L$$

이라고 쓴다.

수열의 극한값

수렴하지 않는 수열$(a_n)$에 대하여 n이 커짐에 따라 $a_n$이 커질 때, 수열$(a_n)$은 양의 무한대로 발산한다(diverges to $\mathrm{\infty }$)고 말하고

$$\underset{n\to \mathrm{\infty }}{lim}{a}_n=\mathrm{\infty }$$

로 나타낸다. 마찬가지로 수렴하지 않는 수열 $(a_n)$에 대하여 n이 커짐에 따라 $(a_n)$이 작아질 때, 수열 $(a_n)$은 음의 무한대로 발산한다(diverges to $\mathrm{\infty }$)고 말하고

$$\underset{n\to \mathrm{\infty }}{lim}{a}_n=-\mathrm{\infty }$$

로 나타낸다.

등비수열 극한

수렴하는 수열의 기본 성질

수열의 극한값을 구하기 위해서는 다음과 같은 사실들을 사용할 수 있다.

극한 성질

수렴하는 수열의 기본 성질

자연상수

자연상수 e는

$$e=\underset{n\to \mathrm{\infty }}{lim}{a}_n=(1+\frac{1}{n}{)}^n$$

로 정의한다.

단조 수열

모든 $n\ge 1$에 대하여

$$a_{n+1}\ge a_n$$

이면 수열 ($a_n$)은 증가수열(increasing sequence)이라고 한다. 모든 $n\ge 1$에 대하여

$$a_{n+1}\le a_n$$

이면 수열 ($a_n$)은 감소수열(decreasing sequence)이라고 한다. 증가수열 또는 감소수열을 단조수열(monotone sequence)이라고 부른다.

유계인 수열

수열 ($a_n$)이 주어졌을 때, 모든 n에 대하여

$$a_n\le M$$

인 실수 M이 존재하면 수열 ($a_n$)은 위로 유계(bounded above)라고 한다. 마찬자기로, 모든 n에 대하여

$$a_n\ge m$$

인 실수 m이 존재하면 수열 ($a_n$)은 아래로 유계(bounded below)라고 한다. 위로 유계이면서 아래로도 유계인 수열을 유계인 수열(bounded sequence)이라고 한다. 수렴하는 모든 수열은 유계이다. 일반적으로 그 역은 참이 아니다. 그러나 단조수열인 경우 유계이면 그 수열은 항상 수렴한다는 것이 알려져 있다.

유계수열

일계선형점화식

초항이 a이고 공차가 d인 등차수열 $(x_n)$은 모든 n에 대하여 다음과 같은 관계식을 만족한다.

$$x_{n+1}=x_n+d$$

또한 초항이 a이고 공비가 r인 등비수열 $(x_n)$은 모든 n에 대하여 다음과 같은 관계식을 만족한다.

$$x_{n+1}=r{x}_n$$

이와 같이 어떤 규칙에 의하여 정의되는 수열은 앞, 뒤 항 사이의 관계식으로 표현할 수 있다. 앞의 항을 이용하여 뒤의 항이 정의되는 식을 점화식(recursive equation)이라고 한다.

다음과 같이 함수 $f$가 일차식인 경우 점화식을 일계선형점화식(first order linear recursive equation)이라고 한다.

$$x_{n+1}=f(x_n)=a{x}_n+b,n=0,1,2,...$$

$n=0,1,2$에 대하여 계산해 보면

$$\begin{array}{rl}& x_1=a{x}_0+b\\ & x_2=a{x}_1+b=a(a{x}_0+b)+b=a^2{x}_0+(a+1)b\\ & x_3=a{x}_2+b=a(a^2{x}_0+(a+1)b)+b=a^3{x}_0+(a^2+a+1)b\end{array}$$

이고 일반적으로 다음 식이 성립한다.

$$x_n=a^n{x}_0+(a^{n-1}+a^{n-2}+\cdots +a+1)b$$

$a\ne 1$이면 두 번째 항은 공비가 a인 등비수열의 합이므로

$$x_n=a^n{x}_0+b\frac{a^n-1}{a-1}$$

이다. $a=1$이면

$$x_n=x_0+nb$$

이다.

일계선형점화식